2025학년도 수능특강 미적분 수열의 극한 기본문제 풀이 유의사항

2025학년도 수능특강 미적분 수열의 극한 기본문제 풀이 유의사항

수능을 준비하는 수험생들에게 학기의 시작은 전투의 시작을 알리는 순간입니다. 오늘 전국 모든 학교가 개학을 했고 이제 겨울방학 중에 달려왔던 결실을 따러 학기에 집중할 시간이네요. 수학하는 킴꼬망이 입니다. 2025학년도 대입을 위해서 수능을 집중하는 학생들도 있고, 내신에 목숨거는 친구들도 있을텐데요. 늘 하는 말이지만 구분해서 달리는 순간 정말 큰 리스크를 안고 가는 것이기 때문에 큰 줄기로보고 실력 올리는데 집중하면 좋을 것 같습니다.

 

오늘은 미적분 첫 파트 수열의 극한에서 기초가 되는 문제들은 넘어가고 오답율이 어느정도 발생할 수 있는 문제를 하나 풀어보고 접근하는 방법에 대해서 알아보도록 하겠습니다.

 

 

목  차

1. 수열의 극한 문제 접근법

2. 풀이법 (문제 해석하기)

3. 해답 구하기 및 다른 풀이법

4. 마무리

 

 

 

 

1. 수열의 극한 문제 접근법 (오답률 30~50)

출처 : 수능특강 미적분

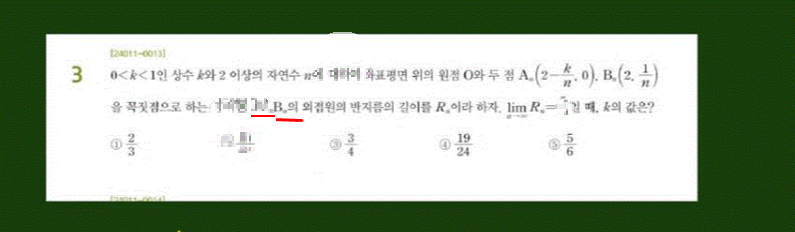
문제는 저작권 문제로 일부 모자이크 처리를 해두었습니다.

 

위 문제는 수열의 극한 끝자락에 나오는 문제입니다. 수능특강에서 실력문제 이전에 기본문제로 유형에 따라서 어려운 3점 문제이거나, 적당한 4점 문제로 변형되서 나올 수 있는 유형입니다.

 

미적분 파트에서 나온 문제이기 때문에 극한이나 미적분에서 개념이 잡히지 않아 틀릴 것이라고 생각하고 미적분에서 해답을 찾으려 하는데요. 

 

미적분에서 대다수의 어려운 문제들은 중3 도형이나 고1 다항식, 도형 파트를 이해하고 접근하는 부분에서 해법이 다 있습니다.

 

즉, 도형을 해결 못하거나 수식을 문제가 원하는대로 도출을 못해서 틀리는 문제가 대다수입니다.

 

위에 예시로 가져온 문제는 기본적으로 단순한 극한이기 때문에 풀이 자체는 2분안에 끝납니다. 하지만 문제 접근하는데 3분이상 소요되는 문제고 헤메거나 잘못짚으면 3점문제임에도 10분이상 소요하게되는 난감한 문제가 될 수 있습니다.

 

맞춘다 하더라고 킬러문제가 아닌 4번에서 시간을 뺏긴다면 풀었다해도 푼게 아닌 셈이되는 슬픈 상황이되는 것 이죠.

 

 

 

2. 풀이법 (문제 해석하기)

 

위의 문제를 뜯어서 해석해보면 결국 Rn을 구해야하는 문제가 되는데, 주어진 문제에서 Rn은 원점을 제외한 두 점이 n에 따라 변하는 외접원의 반지름입니다.

말을 길게 써서 복잡해보이는데, 외접원의 반지름을 n에 관한 수식을 구하면 극한만 취하면 바로 풀리는 문제라는 뜻입니다.

 

삼각형에서 두 점은 변하고 있고, 원점만 그대로 있기 때문에 원의 중심을 구해서. 원점과의 거리공식을 이용해서 거리를 구하면 되는 문제입니다.

 

그러면 다시 돌아와서 외접원의 중심을 구하는 문제가 되는데, 외접원의 중심과 삼각형이 무슨 관계인지를 봐야합니다.

 

삼각형의 외접원은 삼각형 각변을 하나씩 분리해서 생각해보면 단순히 원에 그어진 현에 불과합니다.

 

현의 특징은 원의 중심에서 현에 그은 수선은 현을 이등분한다.

 

그러니까 삼각형의 각 선분의 수직이등분선의 교점이 위 문제에서 외접원의 중심이 됩니다.

 

외접원의 중심을 구하는 문제가 이제는 선분의 교점 문제로 바뀌었습니다.

 

가장 간단한 선분을 찾으려면 당연히 고정점인 O를 끼고 있는 선분 두개를 이용하는 것이 좋습니다. An,Bn은 변하기 때문에 수학에서는 변수를 어떻게 잘 통제하느냐가 문제를 어렵게 끌고가느냐 쉽게 끌고가느냐를 결정하기 때문입니다.

 

그래서 위 풀이를 보면 선분 OAn과 OBn의 중점을 구하고, 기울기가 수직인 직선의 방정식을 구해주게됩니다. 기울기와 지나는 점만 있으면 직선의 방정식을 구할 수 있고

 

직선의 방정식이 두개가 있으니 연립해서 풀면 교점을 찾을 수 있고 그 교점을 Cn이라고 하면 그 Cn읜 외접원의 중심이 되는 것이지요.

 

따라서 원점과 Cn의 거리를 구하면 Rn이 n에 관한 식으로 나오게 됩니다.

 

여기까지가 중등개념+중등개념+중등개념+중등개념 입니다. (원의 중심과 현, 수직이등분선, 직선의방정식, 연립방정식) 중등개념 4번만 엮어놨을 뿐인데 수능 4점짜리 문제가 되는 것입니다.

 

내가 틀렸던 문제가 어디서 틀렸는지 잘 살펴보는 습관은 학습에 매우 중요하니 꼭 오답정리할 때 풀이를 분석해보고 어느 개념이 내가 누락되었는지 보는 것이 중요합니다.

 

 

 

3. 해답 구하기 및 다른 풀이법

위 문제의 마지막 풀이는 극한 취해서 전개해주고 극한값 구하면 끝입니다.

결국 OCn의 길이를 구하는 문제였던 셈입니다. 극한 풀이는 1/무한대 꼴의 극한이 나오기 때문에 전혀 어렵지 않는 극한입니다.

 

보통 무한급수나 수열의 극한, 로그함수를 이용한 수열의 극한 등의 문제들은 결국 이 문제와 전부 맥락이 같은 문제입니다. 식을 찾는 문제인데 식을 찾는데 들어가는 개념은 극한에서 배우는 개념이 아니고 중3과 고1에서 배우는 개념입니다.

 

수능을 보는데 있어서 중3, 고1을 틈틈히 살펴 봐야 하는 이유이지요.

 

 

다른풀이

위 문제의 경우는 삼각함수를 이용해서 풀이하는 방법도 있습니다. 기울기가 tan인 것을 이용해서, Bn이 변하면 기울기가 변하는 성질을 이용해서 접근합니다.

 

그리고 외접원의 반지름을 구하는 문제이기 때문에 사인법칙을 이용해서 R을 구하는 접근을 할 수 있습니다.

 

하지만 삼각함수로의 접근은 어려워서라기보다 기타 다른 문제의 유형들을 접근하는데 크게 도움이 되질 않기 때문에 위의 풀이처럼 도형 성질로 접근을 하는 것이 더 옳은 방향이라고 생각합니다.

 

물론 반박하시는 분들도 계시겠지만 다른 풀이로 푸는것이 틀렸다는 것이 아니라 연습을 하는 입장에서는 더 다양한 문제를 접근 할 수 있는 하나의 키를 보다 완벽하게 다듬는게 시험을 대비하는데 옳기 때문입니다.

 

근의 공식에서 짝수공식을 굳이 외우지 말라고 하는 이유도 같은 맥락입니다. 공식을 잘못 적용해서 실수 하는 경우도 있겠지만 외워야할 공식이 너무 많은데 짝수에만 사용가능한 반쪽짜리는 외울 필요가 없다는 생각입니다.

 

위 유형의 문제들은 도형의 형태로 더 많이 나오기 때문에 도형을 먼저 충분히 익혀가면서 접근하고 삼각비를 이용한 방법은 특화된 문제가 있기 때문에 그 문제를 볼 때 더 깊히 보는 것을 추천합니다.

 

 

 

4. 마무리

수열의 극한에서 정말 기초적인 문제부터 기본이 되는 문제들이 너무 많고, 극한의 성질을 살펴볼만한 것들도 너무 많지만 극한의 문제는 위 유형만 점령해도 어지간한 극한 문제는 거의 풀이가 가능하다고 생각합니다.

 

그런 유형을 집중적으로 공부하고, 가지치기를 하는 것이 시간도 아끼고 고득점으로 가는 방법이니 참고하시고, 힘들어도 참고하세요!!

 

대한민국 모든 수험생을 응원합니다.