2025 수능특강 미적분 삼각함수 미분법 주요 문제 풀이법

수학하는 킴꼬망이입니다. 오늘 미적분 풀이를 해주다가 괜찮은 유형의 문제가 있어서 가져왔습니다. 출처는 수능특강입니다. 좋은 문제이고 유의해야 할 사항이 분명히 있습니다. 문제 안에 들어있는 힌트에도 군더더기가 없고, 모든 힌트를 정말 제대로 써야만 풀리는 문제라서 그렇습니다.
평소 간과 할 수 있는 조건조차도 문제 풀이의 핵심이 되어있는 문제니까 출제자라면 관심 있게 볼 수 있는 문제니 참고하시고 이런 문제를 접근할 때 유의할 부분들을 정리해 보시기 바랍니다.
1. 삼각함수 미분법 기본문제 (난이도 쉬운 4점)

삼각함수를 특히 어려워하는 이유가 공식이 많은 것은 둘째 치더라도 제대로 접근했다고 생각하고 풀이를 했는데 발을 잘못 딛는 순간 무한루프에 빠지는 마법이 걸리기 때문입니다.
계속 돌고 돌고 돌아서 제자리로 오는 경험을 하셨다면 공감이 되시리라 생각됩니다.
이제 조금만 더 경험해 보시면 그 경계점을 넘어설 수 있을 것입니다.
위 문제는 풀이를 진행하면서 답까지 정리가 되었는데 접근법과 유의사항을 소개하려 하는 것이니 참고하시기 바랍니다.
보통 저런 유형의 문제는 첫 줄 조건, 두 번째 줄 조건, 세 번째 줄 문제가 묻는 것으로 나누었을 때 세 번째 줄의 물음을 먼저 해석해서 풀이 방향을 설계합니다.
그리도 두 번째 줄의 조건을 가지고 문제를 해결합니다. 첫 번째 줄의 조건은 그냥 당연하게 주어지는 조건으로 인식하고 풀어도 풀리는 문제가 보통 많은데 이 문제는 첫 번째 줄의 조건이 사실상 가장 중요한 문제라서 끌고 왔습니다.
어떻게 전개되는지 아래에서 계속 이어가겠습니다.
문제의 접근 방법은 동일합니다. 마지막 물음이 무엇인지를 보고 설계를 합니다. 위에 써 놓은 대로 탄젠트의 합을 묻는 문제인데, 탄젠트의 각도 합의꼴로 표현이 되어있습니다.
여기서 공부 좀 하는 친구들은 삼각함수 덧셈정리로 접근해서 해결하려 시도해 보는 친구도 있을 텐데 결론을 말씀드리면 제대로 함정에 걸리고 나락에 빠지게 되는 순간입니다.
일단 한번 써보면 변수가 세 개나 있다 보니 더 어려워지는 결과가 나옵니다. 세 실수를 하나하나 다 구해야 하는데 힌트가 없습니다. 바로 버리셔야 합니다.
그럼 센스 있게 탄젠트의 각을 하나로 보고 풀이를 진행해야 한다는 결론에 도달합니다. 그럼 변수를 두 개로 줄일 수 있기 때문입니다.
수학은 변수를 줄여나가는 과정으로 이해하면 풀이가 조금 더 수월하게 진행될 것입니다.
2. 접근 및 풀이법
문제의 접근은 물음을 잘 보면 알파와 베타가 한 개로 묶여있고, 베타와 감마가 또 한 개로 묶여있기 때문에 변수를 하나씩 제거해서 아래의 꼴로 만들어 줄 수 있을까?라는 생각으로 접근해야 합니다.
두 번째 줄에 있는 조건식에서 감마를 이항 해서 알파 베타에 관한 식을 뽑아낼 수 있습니다.

두 개의 식을 원하는 변수만 남기고 이항 해보면 삼각함수 성질에서 사인제곱과 코사인제곱의 합이 1이 되는 성질을 이용할 수 있어 보입니다.
두 식을 각각 제곱해서 변끼리 더하면 두 번째 식으로 전환되는데 여기서 코사인 덧셈정리가 활용되는 식이 도출되고 더해보니 β-α가 이쁘게 나와줍니다.
이대로 저 각을 통으로 풀이해야지 여기서 탄젠트는 사인을 코사인으로 나눠주는 것이기 때문에 Sin(β-α)를 구해야겠다고 생각하면 또 나락으로 가는 겁니다.
어떤 조합을 시도해도 사인값을 구할 방법이 없기 때문입니다.
결과적으로 코사인 β-α가 -1/2이라는 값을 얻었는데, 자세히 보면 두 번째 γ-β도 식이 동일하기 때문에 굳이 계산을 더 할 필요 없이 Cos(γ-β)=-1/2라는 값을 얻게 됩니다.
그래서 γ-β 와 β-α가 2/3파이 이거나 4/3파이를 갖는다는 것까지는 확인이 가능합니다.
첫 줄 조건에서 세 실수가 2파이보다 작기 때문에 빼준 값은 0과 2파이 사이의 각이 되어서 둘 중 하나입니다.
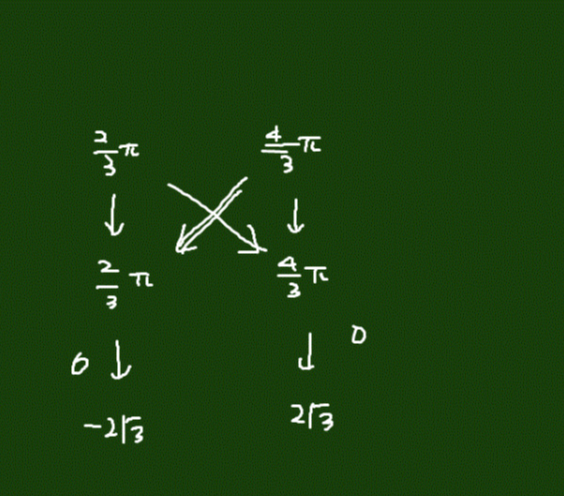
대충 여기까지 진행했으면 보통의 문제는 답이 나오거나 선지에 필요한 해답만 있어서 결론을 낼 수 있는 문제도 종종 있습니다.
하지만 저기서 하나의 조건이 해결되지 않는 순간 위 사진처럼
세 가지 경우가 나옵니다. 탄젠트의 각이 서로 같을 경우와 서로 다를 경우로 나오는데, 각이 서로 다르면 합은 0이 될 것이고 2/3파이로 같으면 -2 루트 3, 4/3파이로 같으면 2루트3이 나오게 됩니다.
중요한 것은 세 가지 경우가 모두 선지에 있다는 것입니다. 찍을 수도 없는 문제인데 수능에 너 오면 33%의 확률에 걸어야 하는 것일까요?
수능에서 결국 조건을 못 찾고 시간만 흐른다면 20%의 확률보단 33%의 확률에라도 걸어야 하는 것이 맞습니다.
그만큼 문제 자체가 어렵다기보다는 그간 다른 문제에 익숙해서 조건이 문제 풀이 자체에는 영향을 주지 않았던 문제들에 익숙했다면 풀이가 굉장히 어려웠을 문제라는 것입니다.
첫 번째 조건이 굳이 α<β<γ를 순서를 두었기 때문에 그 조건을 써야만 문제가 해결됩니다. 조건을 찾고 그 조건이 왜 굳이 디테일하게 주었는지를 생각해봐야 한다는 것이지요.
이쯤에서 각을 뚫어지게 쳐다보다가 β-α, γ-β는 있으니까 γ- α를 만들기 위해서 두 각을 더해 봅니다.

더해보면 γ- α는 각각 2파이보다 작은 각이었고 뺏기 때문에 2파이보다 작은 결괏값이 나오게 됩니다.
다시 더한 식을 자세히 들여다보면 (β-α)+(γ-β) = γ- α <2파이인데, (β-α)나 (γ-β)가 둘 중 하나라도 4/3파이가 되는 순간 합이 2파이와 같아지거나 2파이보다 커져서 모순이 됩니다.
결론은 둘 다 2/3파이가 될 수밖에 없다는 뜻입니다.
일반적으로 풀이를 진행해도 위 조건을 찾지 못한 사람들이 문제를 오랫동안 붙잡고 있거나 포기해서 틀리게 만드는 문제일 것 같고 실제 수능에 출제된다면 오답률 5~60%는 나올 수 있는 문제로 보입니다.
하지만 쉬운 4점이라고 판단한 이유는 조건의 해석만 바로 된다면 시간도 얼마 안 걸리고 답도 깔끔하게 나올 문제라서 그렇게 판단했습니다.
문제를 접근할 때 문제를 잘게 쪼개보면서 하나씩 합쳐서 그림을 완성하는 형태의 훈련을 꾸준히 하길 바라고, 하나의 문제를 접근하더라도 연습할 때는 어떻게 힌트를 조작해야 하는지 고민하는 시간을 충분히 가져보는 것을 추천드립니다.
'수학하는 킴꼬망이 > 미적분' 카테고리의 다른 글
| 미분계수 원과 접선, 접선의 방정식 2문제 (풀이 유의사항) (0) | 2024.03.06 |
|---|---|
| 2025학년도 수능특강 미적분 수열의 극한 기본문제 풀이 유의사항 (0) | 2024.03.04 |

